Recursion

Write a program to calculate power of x:

Method Signature: power(int x, int n)
Purpose: Function should return the power of x^n

1. The first solution is to use the definition that x^n is the number of x multiplied by itself n-1 times.

2. In the second solution, the algorithm paradigm used is divide and conquer. The algorithm is optimized to O(log(N)) by calculating power(x, n/2) only once and store it.

Suppose we want to calculate 2^6. we can calculate it as follow.

if we know 2^3, we can calculate 2^3 * 2^3 to get 2^6.

if we know 2^1, we can calculate 2^1 * 2^1 to get 2^3.

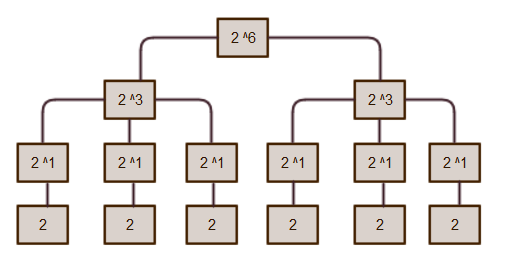
We can define the problem recursively as follow:

y = power(x, n/2) * power(x, n/2) //if n is even

y = power(x, n/2) * power(x, n/2) * x //if n is odd

write a program to sort an array of integers

The algorithm that will be used here is divide and conquer. We have seen in a previous example how to merge two sorted arrays of integers . The idea here is to divide each array in two halves, sort it and then merge the two halves. The division is proceeded recursively.

We start sorting the smallest array in the first half eg.

We stop sorting when there is only one element in the array i.e The array should contain more than one element.

Following is the algorithm

if array contains more than one element

sort the first half of the array

sort the second half of the array

merge the sorted halves

end if

The following show all the calls to mergesort after the initial call mersort(numbers, 0, 6)

mergeSort(A, 0, 6)

mergeSort(A, 0, 3)

mergeSort(A, 0, 1);